介绍#

局部离群因子算法（Local Outlier Factor, LOF） 是一种基于密度比的方法，用于检测数据中的离群点。与以往的离群点检测算法不同，该算法从局部角度考虑，通过密度比来判断数据点是否为离群点。核心思路为： 在规定了局部区域后，离群点区域的密度与周围区域的密度有着较大的差别，因此，通过计算待检测点区域密度与周围区域密度的比值，即可判断该点是否为离群点，如下图：

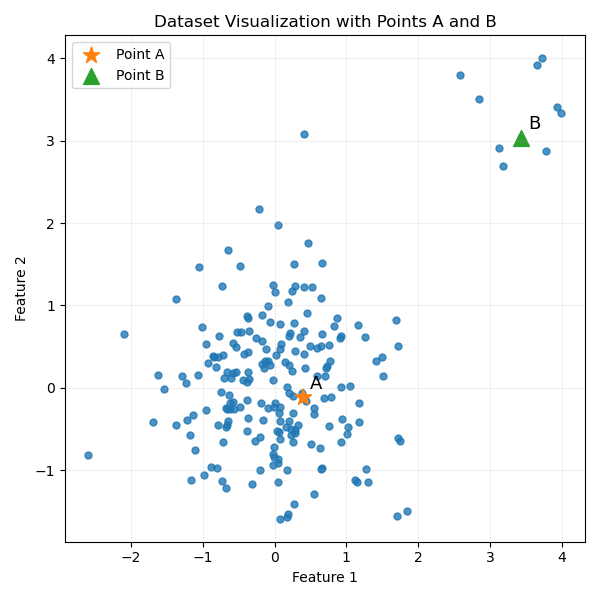
可以明显看出，点B周围的密度较点A周围的密度显著较低，且距离点群较远，因此可以判断点B为离群点（异常点）。在实际应用中离群点的局部密度也显著低于邻居的局部密度，根据这个特性，我们可以判断一个点是否为离群点。

前置知识#

KNN——K邻近算法#

KNN（K Nearest Neighbors） 是一个监督学习分类算法，可以用于分类，也可以用于回归。具体思路为：

确地k值——找距离待检测点最近k个邻居点，k值不同，最终得到的结果也不同
确定距离计算方法，常用的有：

前置背景
设点 $A(x_1,x_2,x_3,……,x_n)$ ，点 $B(y_1,y_2,y_3,……,y_n)$
1. 欧氏距离(Euclidean Distance)： $d_{ab} = \sqrt{(x_1-y_1)^2 + (x_2 - y_2)^2 + \cdots +(x_n-y_n)^2}$
  
  最常用的距离度量，表示两点之间的直线距离。适用于连续数值型特征，但对特征尺度敏感。
2. 曼哈顿距离(Manhattan Distance)： $d_{ab} = |x_1-y_1| + |x_2-y_2| + \cdots + |x_n-y_n|$
  
  也称为城市街区距离，计算各维度绝对差值的和。在高维空间中比欧氏距离更稳定。
3. 切比雪夫距离(Chebyshev Distance)： $d_{ab} = \max\limits_i |x_i - y_i|$
  
  定义为各维度坐标差的最大值。常用于棋盘问题，相当于国际象棋中王的移动距离。
4. 闵可夫斯基距离(Minkowski Distance)： $d_{ab} = (\sum\limits_{i=1}^n |x_i - y_i|^p)^{\frac{1}{p}}$
  
  这是一个距离度量的一般形式：
  - 当 $p=1$ 时，退化为曼哈顿距离
  - 当 $p=2$ 时，退化为欧氏距离
  - 当 $p \to \infty$ 时，趋近于切比雪夫距离
5. 余弦相似度(Cosine Similarity)： $\cos(\theta) = \frac{\sum\limits_{i=1}^n x_i y_i}{\sqrt{\sum\limits_{i=1}^n x_i^2} \sqrt{\sum\limits_{i=1}^n y_i^2}}$
  
  衡量两个向量方向的相似度，而非距离大小。常用于文本分析和推荐系统。
选择建议
- 特征连续且尺度一致：优先考虑欧氏距离
- 特征稀疏或高维：余弦相似度或曼哈顿距离效果更好
- 对异常值敏感：曼哈顿距离比欧氏距离更鲁棒
- 数据需要标准化：使用距离度量前，建议对特征进行归一化或标准化处理
这里由于数据集是简单的二维点集，故使用欧式距离作为距离计算的方法。
计算找到待检测点的K邻近点，然后根据这些邻近点完成想要的操作如预测类别。这里只使用这些邻近点来计算密度

第K距离（K-Distance）#

对于数据集中的任意点P，将其到所有其他数据点的距离按升序排列：

d_{(1)} \leq d_{(2)} \leq \cdots \leq d_{(k)} \leq \cdots \leq d_{(n)}

则第k个距离值 $d_{(k)}$ 称为点P的第k距离，记作 $k\_distance(P)$ 。也就是以P为圆心， $k\_distance(P)$ 为半径画圆，圆内恰好包含k个点（含边界上的点）。

例子：#

假设有点P，其他点按到P的距离排序为：[1.2, 1.5, 1.8, 2.3, 2.7, 3.1, …]

当k=3时：

第1近邻：距离1.2 <- 第1距离
第2近邻：距离1.5 <- 第2距离
第3近邻：距离1.8 <- 第3距离
第5近邻：距离2.7 <- 第5距离

相应的，第k距离也就是第k近邻点距离点P的距离。

第K邻域（K-Distance Neighborhood）#

任取一点P，距离点P的距离小于等于第k距离的所有点的集合，即为第K邻域，记作 $N_k(P)$ 。使用数学表示如下：

N_k(P)=\{Q \in D \setminus \{P\} \mid d(P,Q) \leq k\_distance(P)\}

其中：

D代表整个数据集
$D \setminus \{P\}$ 表示集合D去除子集{P}后的集合，也就是 $D - (D \cap \{P\})$
$k\_diatance(P)$ 表示点P的第k距离
$d(P,Q)$ 表示P和Q的距离

用图表示：

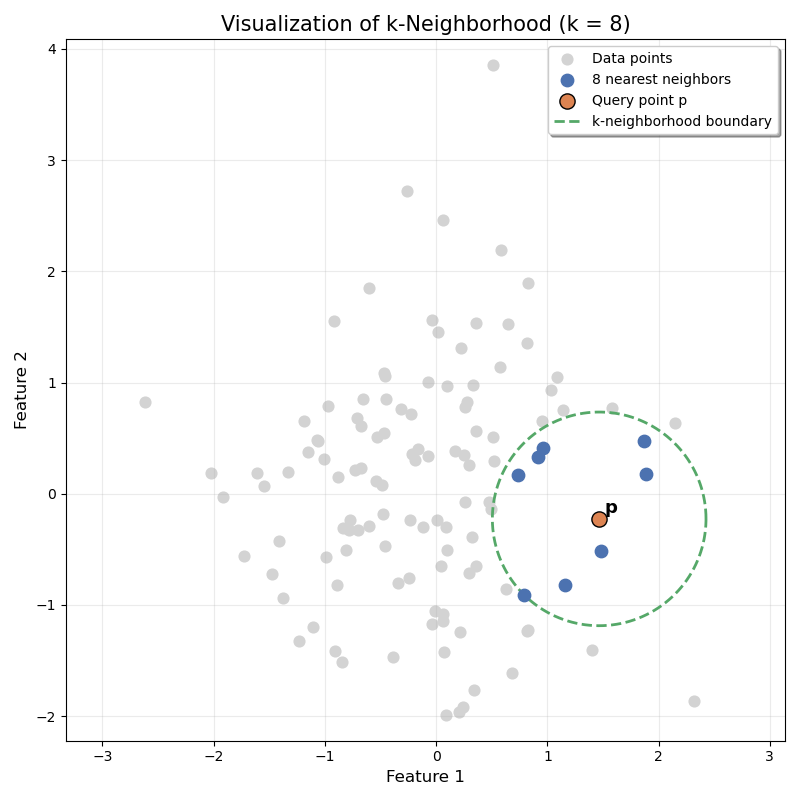
可达距离（Reachability Distance）#

设点O为待检测点，点P为O的第K邻域内的点，则点O与点P的可达距离为：

reach-dist_k(P,O) = \max(k-distance(P),d(P,O))

也就是点 O 到 P 的距离与点 P 的第 k 距离中的较大值。

算法原理#

局部可达密度（Local Reachability Density)#

和平常的密度计算方式相似，局部可达密度（LRD）的计算公式为：

LRD_k(P) = \frac {\left | N_k(P) \right | }{\sum_{O\in N_k(P)}{reach-dist_k(P,O)}}

其中：

$N_k(P)$ 为点P的第k邻域
$reach-dist_k(P,Q)$ 为点P与Q的可达距离

局部利群因子（Local Outlier Factor）#

这是LOF算法最重要的部分，整个算法根据此值来判离群点。思想为：

Info

利群点的局部可达密度一定与正常点的局部可达密度有差异，因此可以通过计算待检测点的第k邻域内的点的局部可达密度与待检测点局部可达密度密度的比值来判断待检测点是否是离群点。

为了确保没有偶然性，计算待检测点第k邻域内的全部点的局部可达密度与待检测点局部可达密度的比值，然后取其平均值做为最终的检测标准，可以在较大程度上鉴别离群点。

注意

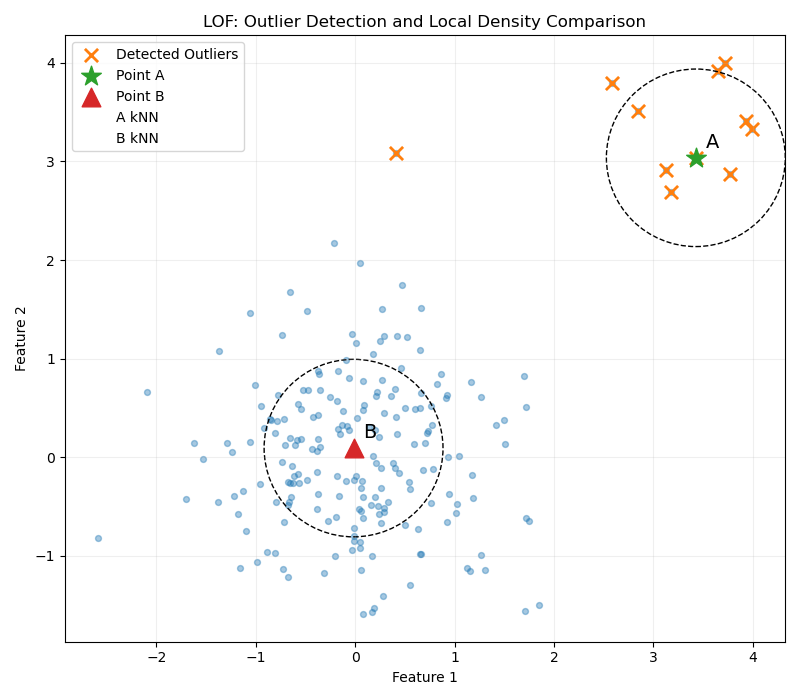
注意，此图仅供教学使用，虚线圆圈出的范围不代表第k邻域，这里只是为了表示方便以让读者真切感受到基于密度的局部利群因子判断离群点的效果。真实的第k邻域如下：

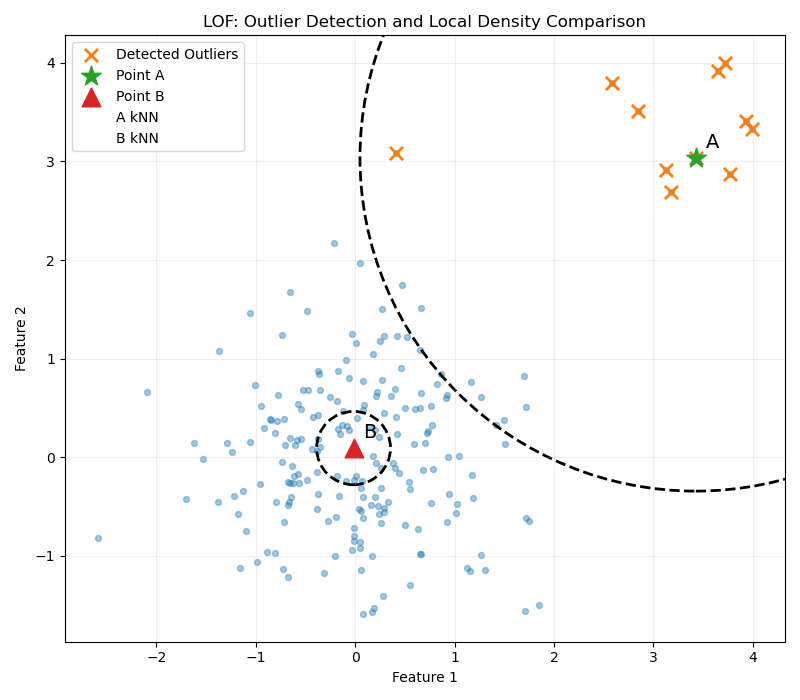
如上图所示，通过局部可达密度可以很好的找出离群点，局部异常因子的计算方式如下：

LOF_k(P) = \frac {\sum_{O \in N_k(P)}{\frac {LRD_k(O)}{LRD_k(P)}}}{\left | N_k(P) \right |}

其中：

P为待检测点，O为点P的第k邻域的点
$N_k(P)$ 为点P的第k邻域

通常认为， $LOF_k(P)$ 这个比值越大于1，表明p点的密度越小于其周围点的密度，p点越可能是离群点；这个比值越小于1，表明p点的密度越大于其周围点的密度，p点越可能是正常点。

算法流程#

1. 确定超参k值#

k值对于LOF非常重要，当 k 较小时，LOF 的局部密度估计不稳定，对噪声敏感，容易导致正常点被误判为离群点；当 k 较大时，局部信息被削弱，异常点可能被周围正常点淹没，从而难以被检测出来。

通常对于中小数据来说，k值在10~20左右较为合理，在此之后，随着数据量地增多以及维度的增大，k值需要适度增大，与此同时可以使用多个k值或者k值区间进行测试，选取效果最好，最稳定的即可。

2. 计算可达密度#

首先使用KNN找到待检测点的第k邻域，然后计算待检测点的可达密度。

对于待检测点第k邻域内的所有点也做和待检测点相同的处理，先找到第k邻域，然后计算可达密度。

3. 计算局部离群因子#

通过LOF的计算公式：

LOF_k(P) = \left ( \frac {\left | N_k(P) \right |}{\sum_{O \in N_k(P)}{\frac {LRD_k(O)}{LRD_k(P)}}} \right ) ^ {-1}

计算待检测点的局部离群因子，然后根据经验，一般来说LOF显著大于1时，认为其为离群点。

常见疑问及解答（Q&A）#

问：为什么要引入可达距离，直接使用距离不行吗？

答：不行。假设检测异常点P且有极少数点非常非常靠近点P，这时如果采用直接距离，局部可达密度（LRD）的计算公式会变为
$LRD_k(P) = \frac {\left | N_k(P) \right | }{\sum_{O\in N_k(P)}d(P,O)}$
易知** $LRD_k(P)$ 会异常边大**，进而导致 $LOF_k(P)$ 会变的非常非常接近0，而根据我们规定的判别条件，此时认为点P是正常点，但实际上P为异常点，这就产生了错误。这种情况称为密度爆炸，如下图（点P为异常点，为方便起见已只绘制点P及其k邻域）所示：

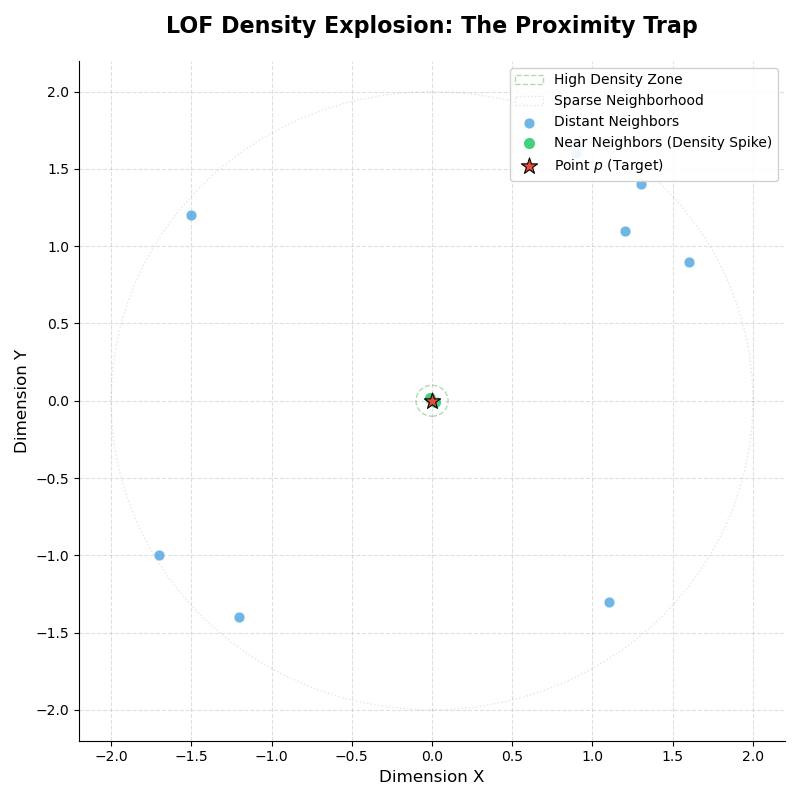
密度爆炸

从图中可以看除有两三个点及其接近点P，而其余点距离点P较远，因此 $\sum_{O \in N_k(P)}{d(O,P)}$ 会被少数及其接近点P的点拉小，从而影响最终的检测结果。

而使用可达距离正是为了解决这个问题，我们规定最小的距离为 $distance_k(P)$ ，从而保证了 $\sum_{O\in N_k(P)}{reach-dist_k(P,O)}$ 不会异常偏小，进而保证了最终检验结果的准确性及正确性。

缺点#

对k值（邻居数）非常敏感
计算复杂度太高，时间复杂度为 $O(n^2)$ ，这在较大规模数据集中无法接受
高维数据效果差：距离趋于相似且局部密度难以区分

我与我周旋久，宁作我

离群点检测——局部离群因子算法

介绍#

前置知识#

KNN——K邻近算法#

第K距离（K-Distance）#

例子：#

第K邻域（K-Distance Neighborhood）#

可达距离（Reachability Distance）#

算法原理#

局部可达密度（Local Reachability Density)#

局部利群因子（Local Outlier Factor）#

算法流程#

1. 确定超参k值#

2. 计算可达密度#

3. 计算局部离群因子#

常见疑问及解答（Q&A）#

缺点#

参考资料#

文章分享

目录